Futher Reading - Microwaves
The Production of Microwaves
Microwaves are produced in medicine using a magnetron generator. The magnetron uses a magnetic field to accelerate electrons in an evacuated chamber. Groups of electrons are accelerated in ballistic cyclonic motion through the magnetron chamber which has cavities lining its outer wall [MW11].
When an electron is accelerated, it will produce electric and magnetic fields which propagate perpendicular to its motion. The electric and magnetic fields are proportional to the electron’s acceleration and thus called an acceleration field, or more usefully known as a radiation field. This is a direct result of Coulomb’s Law [MW7] and it results in the accelerated electrons producing a range of electromagnetic waves which propagate in a toroidal (donut) shape away from the particle.
In the magnetron, the newly formed propagating electromagnetic radiation is incident in the cavities which line the chamber. Here, the waves which have wavelengths of a multiple of 4 lengths of the cavity will resonate. These cavity resonators act as bass-band filters as they collect only a specific band of microwave wavelengths in them through this resonance. These microwaves are then sent through a coaxial cable for medical treatment and imaging.
This is possible due to the practical size of microwaves. In the medical techniques explored on this site, the microwave wavelengths used are in the order of centimetres, this means that the cavities resonator of the magnetron can be made a practical physical size which is easy to build and use in medical contexts.
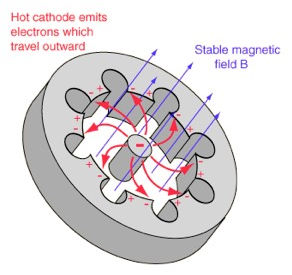
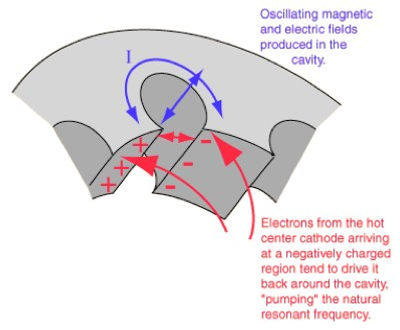
The flow of electrons through a cavity magnetron produces microwaves which resonate in its cavities. Image Source (tobyzerner.com)
Calculation of Heat Energy used for Microwave Ablation

Efficiency Determination:
Microwave ablation of a kidney tumour. Image Source (YouTube.com)
From the literature, it is known that the ablation of a liver tumour of dimensions 4.5cm x 6.0cm x 1.0cm was acted on by a 2.45GHz microwave source at power of 140W for 10minutes. From the relationship Energy = Power x Time we can deduce that a total energy of 45 kJ was applied to the tumour during this treatment [MW3].
For simplicity we have assumed that the treatment was 100% efficient as we compared this energy to the “Tea Scale” and this showed that this specific MW Ablation treatment was analogous to heating up 54% of a cup of tea – where the cup of tea heating calculation can be viewed here
Having assumed 100% efficiency of this treatment, it was realised that the incident energies heated the tumour far beyond the given ablation temperature given as 86°C [MW3]. Thus we can conclude that the heat transfer mechanism is less efficient.
From the heat capacity equation:

Where m is the mass of the liver tumour 0.028 kg, C the specific heat capacity of Liver tissue 3540 J/kg.K (assumed to be constant) [MW8] and ΔT is the change in temperature of the tumour from a body temperature of 37.5°C to 86°C. This yields a required incident heat energy (Q) of 4.87kJ which gives us a procedure efficiency of 11%. This is perhaps due to the dispersion of heat from the tumour into adjacent liver tissues.
Calculation of Heat Energy used for Microwave Tomography
The thermal energy utilised in the passive imaging discussed in Microwave Tomography can be associated with the temperature change which the device is used to detect. The divergence in temperature of the breast tissue from body temperature is 1°C. We can calculate this in terms of energy using Equation 1 similar to that shown above.
Where ΔT is 1°C , m is the mass of the breast tissue which is 0.027kg and C its specific heat capacity which is 2960 J/kg.K [MW8]. The total heat energy (Q) is therefore calculated to be 79.9J.
[The masses of the liver and breast tumours used above were determined using their tissue densities of 1.05 g/cm^3 [MW9] and 1.01g/cm^3 [MW10] respectively and their volumes are both of 2.7cm^3 [MW3]. The tumour volume of breast tissue is an estimation for consistency.]
