Further Reading - Infrared
The Production of Infrared Light
Infrared light is a naturally occurring phenomenon present in all bodies which contain heat energy. Infrared is absorbed and emitted by all molecules in many different ways. This transfer of heat energy causes the molecules to undergo excitations in either of the vibrational, rotational or translational modes. Infrared radiation is integral to heat transfer and the more radiation given to the molecule, the hotter it becomes – as dictated by kinetic theory. Here we can see the water molecule, a molecule made up of one Oxygen atom and two Hydrogen atoms, chemically bonded together. The water molecule, when excited, can undergo translational motion in three dimensions, or the three modes of rotation and vibration as seen above. These excited molecules will eventually emit energy in the form of infrared radiation, which we can detect. A hotter body will emit more intense radiation and bodies at temperatures in and around those which naturally occur on earth, will emit the majority of their energy as infrared.
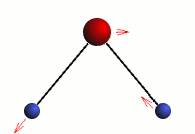
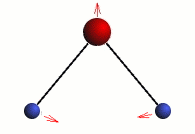
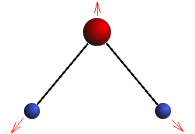
Stretching
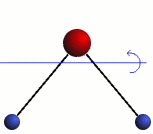
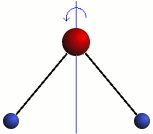
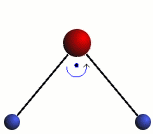
Rotation
The three modes of both the vibration and rotation for a water molecule producing Infrared waves.
From top to bottom: Vibration - Symmetric Stretching, Bending and Asymmetric Stretching. Rotation - X-plane, Z-plane and Y-plane. Image source (Tampa)
Irradiance
The irradiance or intensity of a body is the total power of radiation which is incident on a surface. It can be described using Planck’s Radiation Law as seen below.
This law was first described by Planck in 1900 and is the first example of the quantum theory of energy. From this equation we can see that irradiance is a function of wavelength and temperature. This leads us to the relationship
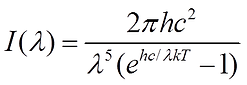
Where I(λ) is the Irradiance in Watts per metre squared (W/m^2), h is Planck’s constant, c is the speed of light, k is the Boltzmann’s constant, T is the temperature in Kelvin and λ is the wavelength.
From this relationship we can plot an irradiance curve over a range of wavelengths and temperatures. From this we see that the curves becomes taller at higher temperatures and that none of the curve lines meet. This means that at any given wavelength of radiation, a body with the highest temperature will be of the highest intensity. Physically, this explains why objects like the human body stand out from their surroundings when imaged using the thermal camera because they are of the highest intensity resulting from their much larger temperature.

Wien's Displacement Law
From the same Irradiance curve, it can be seen that as the temperature of the body increases the peak of its irradiance curve begins to shift towards shorter wavelengths. This can be explained using Wien’s displacement law, which is found by finding the derivative of the Planck Radiation Equation and finding its stationary point. This yields:

The relationship between irradiance and wavelength at different temperatures from the Planck Radiation Law.
Where λpeak is in metres and Temperature in degrees Kelvin (K). The units of the equations are therefore metre-kelvin.
Wien’s Displacement law shows us that the higher the temperature of a body, the shorter its wavelength. This equation was used to determine the specific wavelength of 9.63μm at which the human skin of temperature 27°C or 300.15K will have maximum irradiance.
